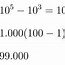
Contoh Soal Rumus Algoritma

Unsur dan Bagian Lingkaran

Merujuk pada buku Matematika Plus oleh Husein Tampomas, jar-jari lingkaran adalah ruas garis yang menghubungkan suatu titik pada lingkaran dengan titik pusatnya. Jari-jari lingkaran dapat didefinisikan sebagai jarak suatu titik pada lingkaran dengan titik pusatnya.

Perhatikan gambar berikut.

Unsur dan Bagian Lingkaran (Matematika Plus/Penerbit Yudhistira)

Jari-jari lingkaran dilambangkan dengan r atau R. Pada gambar tersebut, ruas garis OA = r, OB = r, dan ON = r adalah jari-jari lingkaran dengan pusat O.

Tali busur adalah ruas garis yang menghubungkan dua titik pada lingkaran. Pada gambar tersebut, ruas garis CD dan AB adalah suatu tali busur. Diameter atau garis tengah adalah tali busur yang melalui titik pusat lingkaran.

Dalam gambar tersebut, ruas garis AB adalah diameter pada lingkaran O. Dalam hal ini, dikatakan bahwa A dan B berhadapan diametral. Diameter lingkaran dilambangkan dengan d atau D. Hubungan jari-jari (r) dan diameter (d) pada suatu lingkaran dirumuskan sebagai berikut:

r = 1/2 d atau d = 2r

Apotema adalah ruas garis yang ditarik dari titik pusat suatu lingkaran tegak lurus pada sebuah tali busur. Dapat disimpulkan bahwa apotema adalah jarak titik pusat lingkaran dengan tali busurnya. Pada gambar, ruas garis OM adalah suatu apotema.

Anak panah adalah ruas garis perpanjangan apotema sampai pada busur lingkaran. Garis MN dalam gambar diatas adalah suatu anak panah.

Praktik Kuasai Matematika SD / MI Kelas 4 , 5 ,6

Matematika merupakan salah satu mata pelajaran yang sulit untuk dipahami oleh peserta didik karena soal-soalnya yang menuntut mereka untuk berpikir kritis. Dampaknya terlihat pada nilai USBN mata pelajaran matematika yang lebih rendah dibandingkan dengan mata pelajaran lainnya. Buku Praktis Kuasai Matematika SD/MI merupakan buku penunjang pelajaran matematika kelas 4, 5, dan 6 di sekolah.

Dalam buku ini, terdapat ringkasan materi yang sesuai dengan kurikulum 2013 edisi revisi. Selain itu, di setiap materinya terdapat contoh soal dan pembahasan yang bervariasi. Soal-soal latihan HOTS (High Order Thinking Skill) yang disertai dengan pembahasan yang menyeluruh di setiap materinya juga terdapat pada buku ini sebagai sarana melatih peserta didik dalam belajar secara mandiri. Buku ini ditujukan untuk para peserta didik kelas 4, 5, dan 6 SD/MI sebagai sarana pendukung dalam belajar matematika untuk menghadapi USBN.

Rekomendasi Buku Terkait

Sudut Pusat dan Keliling Lingkaran

Sudut pusat adalah sudut yang dibentuk oleh dua buah jari-jari lingkaran. Ukuran sudut pusat sama dengan dua kali sudut keliling. Sedangkan sudut keliling adalah sudut yang terbentuk dari dua buah tali busur yang berpotongan pada keliling sebuah lingkaran.

Sudut keliling lingkaran dibedakan menjadi:

Rumus Keliling Lingkaran

Sebelum cas-cis-cus langsung menghitung rumus, ketahui dulu mengenai apa itu keliling.

Keliling atau yang disimbolkan dengan huruf “K” adalah panjang seluruh garis batas lingkaran.

Rumus untuk menghitung keliling lingkaran yaitu sebagai berikut:

Jika sebuah lingkaran diketahui jari-jarinya, pakailah rumus K=2.π.r. Namun, jika sebuah lingkaran diketahui diameternya, pakailah rumus K=π.d.

Selanjutnya, ada juga unsur lingkaran yang bernama “luas” (L), tidak lain yakni jumlah daerah yang dilingkupi oleh lingkaran.

Rumus untuk menghitung luas lingkaran adalah:

Rumus Pocket Matematika SD/MI Kelas 4, 5, 6

Buku ini disusun untuk menjawab kebutuhan siswa SD maupun MI dalam rangka mempersiapkan diri dalam menghadapi soal mata pelajaran Matematika dalam Ujian Sekolah. Semua siswa pasti menginginkan nilai ujian yang bagus dan memuaskan. Namun, untuk meraih prestasi hasil belajar yang baik tidak semudah membalikkan telapak tangan. Siswa yang sukses mendapatkan nilai ujian yang tinggi biasanya secara konsisten menerapkan serangkaian strategi produktif dengan tujuan mencapai prestasi akademik yang memuaskan, baik itu dalam belajar maupun praktik pelajaran tersebut.

Tata letak yang menarik dan rinci menjadikan buku ini menyenangkan dan informatif untuk dibaca setiap saat. Ukuran buku yang kecil dan mudah digenggam menjadikan buku “Pocket” ini dapat dibawa kemanapun dan kapanpun sebagai sarana belajar.

Oleh karena itu, buku ini disusun agar membantu siswa mendapatkan nilai terbaik di mata pelajaran Matematika. Buku ini juga dilengkapi dengan bonus Aplikasi USBN Android yang ada didalam Play Store dan bisa Grameds unduh. Sebuah aplikasi simulasi yang dikemas menarik dalam wadah media interaktif untuk mempersiapkan siswa-siswi dalam menghadapi Ujian Sekolah. Grameds bisa memantau berapa lama waktu yang dibutuhkan dalam menyelesaikan latihan soal, baik untuk mengasah kecepatan dan ketepatan Grameds dalam ujian nanti. Grameds bisa melihat nilai rata-rata secara keseluruhan dan juga membagikan hasilnya kepada teman-temanmu melalui akun sosial media, email, dan chat!

Skollamate, ketika pertama kali mendengar lingkaran, apa yang ada di pikiranmu? Hmm… Ban sepeda, kancing, jam dinding, atau pizza? Betul! Pasti kamu bisa menyebutkan banyak benda berbentuk lingkaran.

Tahukah kamu kalau benda yang kamu sebutkan tadi adalah gerbang dari sebuah konsep ilmu Matematika?

Ya! Tanpa kamu sadari, dulu kamu mengenal lingkaran hanya sebagai jenis “bentuk”. Tapi sekarang, kamu akan mengenal lingkaran lebih jauh lagi sebagai salah satu dari konsep Matematika, yaitu “bangun datar”. Menarik, kan?

Nggak sebatas bentuknya melingkar, kamu akan lebih tau serba-serbi tentang lingkaran. Kamu juga bakal ketemu rumus lingkaran yang nggak cuma ada satu. Penasaran mau pelajarin lebih lanjut? Yuk, baca di artikel ini!

Pengertian Periode Gelombang

Periode gelombang adalah waktu yang diperlukan untuk menempuh satu gelombang. Sama dengan periode getaran, periode gelombang juga dalam SI satuannya detik atau sekon.

SCROLL TO CONTINUE WITH CONTENT

Persamaan untuk menentukan panjang gelombang lebih mudah diamati dari gelombang transversal dan persamaannya juga dapat berlaku bagi gelombang longitudinal.

Satu gelombang pada tali didefinisikan terdiri atas puncak dan satu lembah, sebuah puncak gelombang bergerak sepanjang satu panjang gelombang dalam satu periode.

Waktu yang diperlukan untuk menempuh satu panjang gelombang disebut periode dengan lambang (T), sedangkan banyaknya gelombang yang melalui sebuah titik setiap satuan waktu disebut frekuensi (f).

Rahasia Pintar Rumus-Rumus Matematika SD Kelas 3-6

Buang jauh-jauh pikiran jika matematika adalah mata pelajaran ganv sulit. Penting untuk mengatur mindset serta meyakinkan diri sendiri bahwa matematika bukanlah hal yang rumit serta dapat dipahami. Sugesti yang baik pastinya dapat membuat diri sendiri lebih termotivasi untuk belajar matematika dan tak mudah menyerah jika menemukan materi yang sulit. Ingatlah bahwa matematika sangat diperlukan untuk kehidupan sehari-hari, sehingga matematika juga perlu dipelajari.

Buatlah catatan rumus dengan jelan dan rapi dalam buku catatan favoritmu. Ada penelitian yang menjelaskan bahwa mencatat bisa memberikan manfaat untuk meningkat daya ingat, karena terdapat proses pengolahan materi yang didapatkan menjadi catatan dengan bahasa Grameds sendiri. Selain itu, proses pembelajaran yang dilakukan pastinya menjadi lebih efektif karena tak harus membolak-balik buku materi hanya untuk mencari satu rumus.

“Buku Pintar Rumus-Rumus Matematika SD” menyajikan kumpulan berbagai rumus matematika dengan dipadu oleh penjelasan serta contoh soal dan pembahasannya. Berkat metode penyajian materinya yang ringkas, jelas, sistematis, serta mudah dipahami buku ini akan bisa memudahkan para siswa sekolah dasar untuk memahami serta menguasai pelajaran Matematika dengan cepat dan tepat.

Modus Data Tunggal

Untuk data tunggal, detikers dapat langsung melihat nilai yang sering muncul.

Tentukan modus dari skor kuis masing-masing kelompok berikut!

Kelompok a: 20, 3, 30, 10, 12, 15, 25, 10Kelompok b: 21, 12, 12, 30, 31, 5, 10, 10, 35Kelompok c: 30, 12, 11, 8, 7, 10, 10, 30, 11, 5, 9Kelompok d: 5, 3, 30, 10, 18, 33, 50

Kelompok a: modusnya adalah 10.Kelompok b: modusnya terdapat ganda yakni 10 dan 12.Kelompok c: modusnya jamak yaitu 30, 11, dan 10.Kelompok d: tidak memiliki modus

[email protected] https://teknokrat.ac.id/en/ https://spada.teknokrat.ac.id/Read less

KOMPAS.com - Modus adalah anggota yang paling banyak muncul dalam suatu himpunan.

Dilansir dari buku Kumpulan Rumus Matematika SMA (2008) oleh Sri Lestari, modus pada data tunggal adalah data yang mempunyai frekuensi terbanyak.

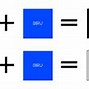
Pada data dengan distribusi frekuensi berlaku rumus sebagai berikut:

Tb = tepi kelas bawah modusi = panjang intervala = frekuensi modusb = selisih frekuensi (modus) dengan kelas sesudahnya

Baca juga: Kumpulan Soal dan Jawaban Mencari Mean, Median, Modus pada Data Nilai Matematika

Dilansir dari buku Cerdas Belajar Matematika (2008) oleh Marthen Kanginan, untuk statistik data tunggal, modus adalah datum yang paling sering terjadi atau datum dengan frekuensi terbesar.

Untuk statistik data berkelompok, Anda dapat menaksir modus dari tabel distribusi frekuensi data berkelompok.

Modus dari data berkelompok dapat ditaksir dengan menggunakan rumus berikut:

Tb = tepi bawah kelas modus (kelas interval dengan frekuensi terbesar)Δf1 = selisih antara frekuensi kelas modus dan frekuensi tepat satu kelas sebelum kelas modusΔf2 = selisih antara frekuensi kelas modus dan frekuensi tepat satu kelas sesudah kelas modusp = panjang kelas interval pada kelas modus

Baca juga: Pengertian dan Rumus Mean, Median, Modus Pada Data Berkelompok

Tinggi badan siswa (cm) dalam suatu kelas sebagai berikut:

Jadi, modusnya adalah 150,32.